

Teori behandlas på sida 3 i PhyWe's handledning och i kap. 15 av Atomfysikens grunder. Förberedelseuppgift: Jönsson problem 15.3 och 15.4.
 | De ringarna som man ser i en Fabry-Pérot etalong är egentligen exempel på fransar av konstant lutning. Man kan se sådana interferensfransar i monokromatisk ljus, till exempel i reflektion av lysrör i overhead-transparenter. |
Studera Zeemaneffekten först kvalitativt. Tittar man med etalongen genom borrhålen i magnetens polskor (longitudinalt), ser man att magnetfältet delar upp ringarna i två komponenter. Men tittar man vinkelrät på fätlinjerna (transversalt), finns det tre komponenter. Kolla komponenternas polarisationstillstånd. I longitudinal riktning är komponenterna cirkulärt polariserade - hur kan du visa det?
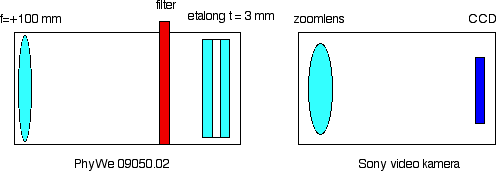
För kvantitativa data använder vi en Sony videokamera med zoomlins istället för PhyWe's mätteleskop. Uppställningen blir enkel, och det går mycket snabbt att ta data. Kameran står på stativ ganska nära Fabry-Pérot etalongen. Kameran ska vara inställd på manuell fokus - ringarna ligger vid ∞. För att få smala ringar är det nödvändigt att reducera exposure för hand till topparna inte är mättade.
Det är enklast att ta data i transversal geometri med polarisationsfilter. Men ringarna verkar vara bredare med än utan fält. Om det beror på fältinhomogeniteter, kan man ta in ljus från områden med mer homogent fält genom borrhålen i polskorna. Tala högt om strömstyrkan när du spelar in bilderna. Eftersom datatagningen går så snabbt, kan man gå till mycket högre strömstyrkor (under kort tid - kolla att spolarna inte blir för varma).
Efteråt kan man ladda ner filmen från kameran till dator med programmet iMovie. Det finns en möjlighet att spara bildrutor som .pict-fil. Gör det för varje fältstyrka. Sedan kan man öppna bilderna i t ex GraphicConverter för att anpassa ljusnivåerna eller konvertera till svart-vit-bild. Man kan mäta ringarnas diametrar på olika sätt: med linjal på skärmen eller på utskrift, med "position information" i Graphic Converter, eller man kan försöka ta fram intensitet längs en linje genom ringarnas centrum, som nedan.

De absoluta värdena för ringarnas vinklar θ är inte viktiga. Syftet med nästa steg i datareduktionen är att få fram fasskillnaden mellan Zeemankomponenterna vid θ=0. Därfär plottar man ringnummer p som funktion av θ² och extrapolerar till θ=0. Ur figuren nedan framgår att man i bilden ovan har Δε = 0,249±0,022. Det betyder att skillnaden i vågtal är Δε/2t = 0,249/(2×0,3) = 0,415 cm-1 (t är etalongens längd). Skillnaden i svängningsfrekvens vid denna fältstyrka är Δν = c Δε/2t.

Bestäm Δε vid θ=0 för fyra fälstyrkor. Plotta Δε (med felgränser) mot B och bestäm proportionalitetskonstanten mellan Δε och B och dess statistiska fel. Jämför med litteraturvärde i joule/tesla, i Hz/T eller i vågtal per tesla. Diskutera möjliga felkällor.