FriElektron.nb

Kvantgas av fria elektroner

Fermi-energin

Många egenskaper av metaller kan man kvalitativt förstå med en enkel kvantmekanisk modell, som ger mycket bättre svar än den klassiska modellen. Först måste man ta med att man kan inte ha fler än två elektroner (spin-1/2 partiklar, fermioner) i samma tillstånd. Det ger teorin vid T=0, och även i första approximation vid rumstemperatur. Sedan måste vi tillämpa kvantmekansika formler för statistisk fysik för att se vad som händer vid T>0.

Vid T=0 befinner alla elektroner sig i lägst möjliga tillstånd. Men eftersom det inte kan finnas fler är två elektroner i samma tillstånd, har många elektroner ganska hög kinetisk energi. (Det är samma sak som i en Na atom - om 1s, 2s och 2p är fyllda, måste den elfte elektron gå i ett 3s-tillstånd.)

Om vi har en kub av till exempel aluminium som är 1 cm^3 stor, innehåller den ungefär elektroner. Vi kan betrakta dem som fria inuti kuben, men de kan inte komma ut. Det handlar alltså om partiklar i en 3-dimensionell låda.
Varje tillstånd har tre kvanttal (,,), och tillståndets energi ges av

In[1]:=

$nvec = {n_x, n_y, n_z} ; En[nvec_] = (ℏ^2π^2)/(2 m L^2) nvec . nvec$

Out[2]=

där L är kubens längd och m elektronernas massa.

Vi kan ett tillstånd alltså beskriva med en tillståndsvektor i en abstrakt matematisk rymd, där tillståndets energi är proportionell mot kvadratet av tillståndsvektorns längd.
Nu kan vi bestämma i vilka tillstånd elektronerna befinner sig. Det finns en högsta nivå för elektronerna energi, och den ger en radie i den här abstrakta n-rymden. Antalet tillstånd Nts med energin av innanför denna radie R= är en åttondel av sfärens volym (det finns bara tillstånd i oktanten där , är positiva, se också Fig. 4-22 i Turton)

In[3]:=

Out[3]=

Vi kan nu bestämma energin En på de snabbaste elektronerna genom att likställa antalet tillstånd med hälften av antalet elektroner som vi har i vår metallkub, vars volym V är lika med .

In[4]:=

Out[5]=

${En (3^(2/3) Nel^(2/3) π^(4/3) ℏ^2)/(2 m V^(2/3))}$

Vi ser att lösningen bara beror på koncentrationen n = Nel/V av elektronerna i materialet. Den här högsta energin kallas för Fermi-energi. Om man ger elektronkoncentrationen n i , blir Ef i elektronVolt lika med

In[6]:=

I aluminium blir det 11,7 eV, i koppar 7,0 eV, i kalium 2,1 eV. I metaller är det alltså en energi långt högre en den termiska energin kT vid rumstemperatur. Man kan också säga att koppar har en fermi-temperatur Ef/k på 82000 Kelvin. Det betyder att den klassiska elektrongasteorin inte är särskilt tillämplig för metaller. Eftersom elektronernas energi är ungefär två tiopotenser större än kT vid rumstemperatur, är elektronernas hastighet typ 10 gånger större än vad man räknar ut för ett klassiskt elektrongas.
I halvledare däremot är elektrontätheterna mycket mindre, och där är fermi-temperaturen ofta mycket lägre än rumstemperaturen. Det betyder att elektronernas energi kan följa en Boltzmann-fördelning, så att den klassiska teorin fungerar väl.

Tillståndstäthet (DOS)

Vi är också intresserade av hur antalet tillstånd i en liten energi-intervall (tillståndstätheten, "density of states", DOS) varierar som funktion av energi. I n-rymden är anatalet tillstånd i ett skal av tjocklek dR vid radie R lika med

In[7]:=

R = Sqrt[En/(ℏ^2π^2)/(2 m L^2)] ; DensityOfStates = 1/8 × 4 π R^2D[R, En]

Out[8]=

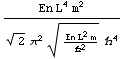
(En L^4 m^2)/(2^(1/2) π^2 (En L^2 m)/ℏ^2^(1/2) ℏ^4)

In[9]:=

Out[9]=

eller ännu enklare ( En ≠ 0 )

In[10]:=

Out[10]=

Tillståndstätheten i ett fritt elektrongas är alltså proportionellt mot roten av energin. Det ger en parabelisk band, som ser ut så här (tillståndstäthet som funktion av energi):

In[11]:=

$DOS [Enr_] := Sqrt[Enr] ; DensityOfOccupStates[Enr_] := DOS[Enr] /; Enr X ... /; Enr > Ef ; Ef = 3. ; Plot[{DOS[Enr], DensityOfOccupStates[Enr]}, {Enr, 0, 5}] ;$

[Graphics:HTMLFiles/FriElektron_25.gif]

Sådana band kan man mäta med röntgenemissionsspektroskopi eller med fotoemissions-spektroskopi. Redan i 1930-talet hade Skinner i USA och Manne Siegbahn i Sverige registerat sådana spektra. De stämde (med experimentell förbredning förstås) väl med formen här nere. Också bandbredden stämde bra med fri-elektronmodellen, i alla fall för enkla metaller som natrium, kalium, magnesium, aluminium.

In[16]:=

OccupiedStates = Polygon[Table[{En, DensityOfOccupStates[En]}, {En, 0, 3.3, 0.01}]] ; Show[Graphics[OccupiedStates], DefaultColor->RGBColor[0, 0, 1]] ;

[Graphics:HTMLFiles/FriElektron_27.gif]

Elasticitetsmodul (Bulk modulus)

Vi ser att Fermi-energin går upp, när densiteten blir högre. Det finns alltså ett motstånd mot kompression.
OBS: det beror i den här modellen inte på att elektronernas Coulombavstötning från varandras lika laddningar.

Vi kan räkna elektronernas medelenergi. Nämnaren ger antalet elektronen, täljaren deras energi:

In[18]:=

Out[18]=

Termodynamisk gäller att tryck P = -. Vi såg tidigare

In[19]:=

Out[19]=

${En (3^(2/3) Nel^(2/3) π^(4/3) ℏ^2)/(2 m V^(2/3))}$

att energin är proportionellt mot . Det ger

In[20]:=

P är alltså proportionellt mot .

Vi kan nu räkna ut kompressibiliteten K eller elasticitetsmodulen B=1/K, som är definierad som

In[21]:=

In[22]:=

Out[22]=

som är lika med

In[23]:=

Elektrongaset är förstås inte det enda som bidrar till elasticitetsmodulen, men den är av samma storleksordning än andra bidrag. För litium räknar man ut 24 GigaPascal , man mäter 11,6 GPa. I cesium som är mycket mjukare stämmer det av en tillfällighet: man räknar 1,54 GPa, man mäter 1,43 GPa. Men i aluminium räknar man 228 GPa, man mäter bara 76 GPa.

Created by Mathematica (November 22, 2004)