Det är ganska enkelt att förstå varför en vakuumrör-diod leder ström åt bara ett håll. Glödkatoden värms nämligen upp till temperaturer där termionisk emission blir stor - elektronerna dunstar av. Dessa elektroner kan dras till katoden av ett elektriskt fält bara om anoden är mer positiv än glödkatoden. Dessutom finns det bara en typ av laddningsbärare: elektroner.
Analysen av en halvledardiod är mycket mindre intuitiv. Verkningen beror på att p- och n-dopat material fogas ihop. Det finns alltså två typer av laddningsbärare: elektroner och hål. Elektriska fält ger upphov till driftströmmar och koncentrationsgradienter ger upphov till diffusionsströmmar av båda typer av laddningsbärare. Vi ska se att elektrisk ledning i en framspänd halvledardiod beror på diffusionsströmmar. Men först ska vi analysera pn-övergången utan pålagd spänning.
Man kan tänka sig att man gör en pn-övergång genom att foga samman en stav p-dopat material med en stav n-dopat material. Laddningsbärarnas slumpvandring gör att de följer koncentrationsgradienten. Men de hål som hamnar i n-materialet rekombinerar snabbt med elektronerna där. Det uppstår ett område nästan utan laddningsbärare på n-sidan. Området är positivt laddat på grund av att de positiva jonerna från donoratomerna är kvar. På samma sätt finns det ett negativt laddat område på p-sidan.
Hela området kallas för utarmningskikt eller depletion layer. Det brukar vara några mikrometer brett, bredare än laddningsbärarnas fria väglängd. Om pn-övergången är abrupt, kan vi approximera området med konstanta laddningstätheter på ömse sidor om övergången med längder ℓp på p-sidan och ℓn på n-sidan. Den totala laddningen måste förstås vara noll, så att
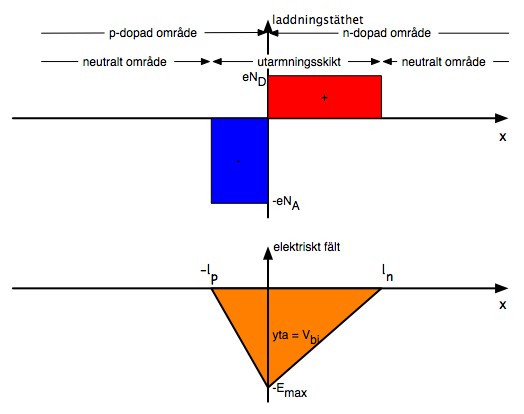
I en graf av laddningstäthet som funktion position måste båda laddade områdenas ytor alltså vara lika stora.
Hittils har jag följt Turton. Men istället för att som han använda Poissons ekvation (en andra-grads differentialekvation), ska jag göra några mellansteg och använda Gauss lag för att få fram det elektriska fältet. Eftersom övergångens tvärsnittsyta är stor jämfört med utarmningskiktets tjocklek, ser vi inget fält utanför övergången - utarmningskiktets totala laddning är noll, och vi kan jämföra laddningsfördelningen med den i en kapacitans. Vid övergången är fältet stort, typ 105 V/cm, och riktat från den positiva laddningen i det n-dopade området till den negativa laddningen i det p-dopade området. Fältets negativa tecken i figuren betyder alltså att fältet är riktat till vänster. Fältstyrkan är en integral över laddningen, och ett konstant värde för laddningen ger en fältstyrka som varierar proportionellt med avståndet till övergången.

Nästa steg är att integrera fältet för att få potentialen. Potentialen ser ut som grafen i Turtons figur 6.3b. Vi får då en inbyggd potential Vbi (eller φ) mellan p-sidan och n-sidan, med storleksordning 106 V/m × 10-6 m ≈ 1 V. Potentialskillnaden är ytan av triangeln i fältstyrke-grafen:
En kort stund efter att p-sidan och n-sidan har fått kontakt, upphör utarmningsområdet att minska. Fältet ger en driftström av minoritetsbärare åt andra hållet, och när diffusionsströmmen har minskat tills att den är lika stor som driftströmmen, har en jämnvikt inställt sig. Då måste Fermi-nivån (eller kemisk potential) på båda sidor vara lika. Det finns då också ett annat sätt att bestämma Vbi. Kontaktpotentialen är skillnaden i Fermi-nivå mellan p- och n-sida:
Genom att likställa dessa, kan man bestämma utarmningskiktets bredd ur koncentrationen av donoren och acceptorer.
Vid backspänning ökar det elektriska fältet över pn-övergången. Men eftersom fältet redan var stort, påverkar denna ökning inte driftströmmen, som är liten eftersom det bara finns några få termiskt genererade minoritetsbärare som hamnar i utarmningsskiktet. Diffusionsströmmen minskar. Den totala strömmen i spärriktningen är alltså liten.
Men spänningsskillnaden mellan p- och n-sidan ökar, så ytan av triangeln in grafen av fältstyrka mot position måste också öka. Både fältstyrkan Emax och utarmningsskiktets bredd W är proportionella mot √(Vbi + Vback). Det finns en gräns för fältstyrkan, där det sker genombrott. Det är inte nödvändigtvis destruktivt - det är så som Zenerdioder kan fungera.
Wie har en utmärkt diod applet som visar hur de fyra olika komponenterna av strömmen beror på den pålagda spänningen.
En framspänning minskar potentialskillnaden mellan båda sidor. Det finns nu fler tillstånd med rätt energi för majoritetsbärarna från andra sidan att slumpvandra till. Diffusionsströmmen ökar exponentiellt med den pålagda spänningen. Driftströmmen är fortfarande oförändrad. Så vi har Idiff = I0 exp(eV/kT). Vid V=0 är det lika stor som driftströmmen, alltså Idrift = -I0. Det leder till diodekvationen:
där I0 självklart beror på Egap och på kT.