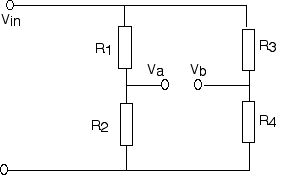
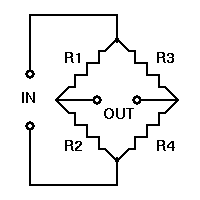


Egentligen består en Wheatstone brygga av två parallella
spänningsdelare.
Potentialen Va =
R2/(R1+R2) Vin =
Vin/(1+R1/R2).
Likadan gäller att potentialen Vb =
Vin/(1+R3/R4).
Bryggan kallas balanserad om spänningen Vab = Va-
Vb = 0.
Då måste gälla att förhållanden mellan
motstånden i båda grenar är lika: R1:R2=
R3:R4.
Vi tar nu en AC ingångsspänning och ersätter R1 med en parallelkoppling av en spole och en kapacitans. Eftersom R3/R4 är fortfarande reell, är Vb i fas med Vin. Då är det enda sättet att få bryggan i balans om kapacitansens negativa reaktans -1/(ωC) är lika stor som spolens positiva reaktans ωL. Det är det enda sättet att få Va i fas med Vb, så att man kan få Vab = 0. (PhyWes brygga ser lite annorlunda ut, men principen är densamma: Va och Vb måste vara lika stora och i fas med varandra.)
Nu är det så att spolens induktans ändras lite när ett yttre magnetfält ger de oparade elektronerna i DPPH en resonansfrekvens som stämmer med fältet is spolen. Även om ändringen är liten, kan ändringen i Vab vara mycket stor. Det är därför man detekterar ESR lätt med Wheatstone-brygga.
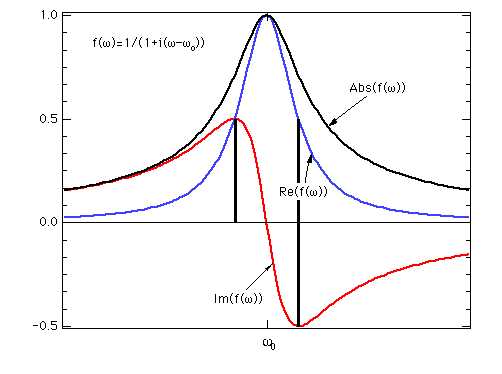
Beroende på inställningen, mäter man i fas eller 90° ur fas med fältet i spolen. Så kan man se den dispersiva signalen (den röda kurvan i figuren ovan) eller den absorptiva signalen (den blåa kurvan). Den dispersiva signalen kan vara lämplig för att mäta resonansens bredd med.
 |
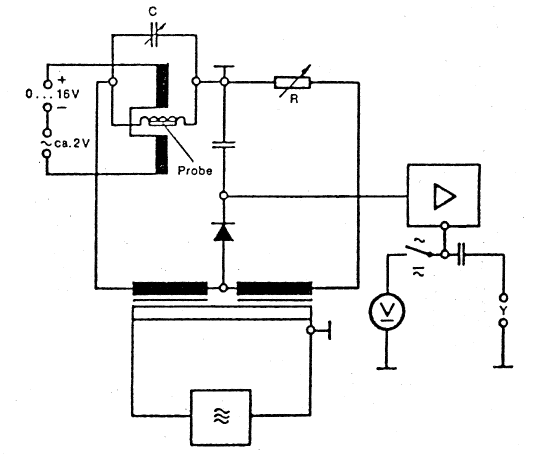 |
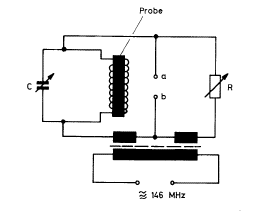
PhyWe's brygga är fördelad över två enheter. Den ena spänningsdelaren befinner sig i styrenheten som innehåller högfrekvent-oscillatorn. Bryggans andra gren befinner sig i resonator-enheten, och består utav en parallellkopplad LC-krets i serie med ett motstånd.