
I det här labbet ska vi kontrastera absorption av alfa-strålning mot absorption av gammastrålning. Alfa-strålning består av partiklar, heliumkärnor, med hög kinetisk energi. De kommer från tunga positiva atomkärnor, där deras potentiella Coulomb-energi är hög (5 MeV eller så). När dessa partiklar färdas genom luft, förlårar de energi genom att jonisera luftmolekyler. De bromsas upp på ungefär samma sätt som en bil som stannar.
Gammastrålning däremot är elektromagnetisk strålning med extrem hög frekvens, och den kan också beskrivas som fotoner. Men fotoner färdas alltid med samma hastighet c. De förlårar inte heller energi på vägen (det är fortfarande samma frekvens och "färg"). Om hälften har blivit absorberad i något material med tjocklek τ½, har fotonerna som kommit inte blivit "tröttare" för det. En platta till med tjocklek τ½ absorberar inte hela resten, men igen bara hälften. Absorption av fotoner är en slumpprocess. Intensiteten avtar då exponentiellt I = Ioe-μx, där μ=ln 2/τ½ är den linear absorptionskoeffienten. Det är Lamberts lag, samma formel som för synligt ljus och annan elektromagnetisk strålning. Skillnaden är bara att gammastrålning växelverkar mycket mindre med materia än synligt ljus, så att halveringstjockleken τ½ är mycket större för röntgen och gammastrålning.

Mätinstrument är en GDM15 med alfa- och betadetektor (den röda lådan på bilden). Alfa-källan sitter på en lång stav och består av americium-241, samma grundämne som i brandvarnare. Isotopens halveringstid är 432 år och alfa-energin är 5,5 MeV.
Detektorn är en ytbarriärdetektor. För varje alfapartikel ger den en puls vars höjd är proportionell mot alfapartikelns kinetiska energi. Pulserna sorteras på höjd i en MCA (Multi-channel analyzer, den svarta lådan). På datorn kan man då se en graf av alfa-partiklarnas energifördelning.
Om man ökar avståndet mellan det radioaktiva preparatet och detektorn, blir energiförlusten i luften större. Den energi som detekteras blir alltså lägre. Enligt Born-Bethe-formeln minskar energin per längdenhet invers proportionellt mot partikelns energi. Partiklarnas energiförluster är alltså störst mot slutet av deras räckvidd, när den kinetiska energin är liten. Denna topp i grafen av energieförlust mot avstånd kallas Bragg peak. Se även en .pdf-fil.
Den radioaktiva källan som undersöks är 241Am med en aktivitet på 10 kBq.
Slå på datorn. Operativsystemet är MSDOS. Ge kommando CD DAS för att komma i mappen DAS. Ge sedan kommando AUTODAS för att starta datainsamlingsprogrammet. Slå på MCAn (den svarta lådan).
Placera alfakällan i den röda detektionslådan så långt in som möjligt. Ställ förstärkaren i läge "α". Starta datainsamlingen med kommando STA. I histogrammet på datorskärmen ska det nu växa upp en topp någonstans på histogrammets högre halva. Om det är tillräckligt många counts (efter några sekunder), kan du stoppa insamlingen med kommando STO. Drag nu ut preparatet en halv centimeter. Starta insamlingen, mät och notera avståndet, och stoppa insamlingen när toppen i spektret är ungefär lika stor som den förra. Upprepa detta förfarande med preparatet utdraget i ytterliga några steg om en halv centimeter.
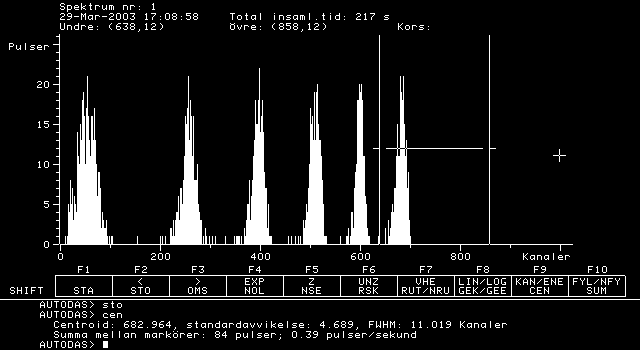
Tag reda på centroiden för topparna i spektrumet genom att markera
den med vänster- och högerklick på musen.
Kommandot CEN ger då kanalen för tyngdpunkt av den delen av
toppen som ligger ovanför linjen mellan markörerna. (I bilden ligger
markörerna lite höga; det hade varit bättre att ha dem på x-axeln.)
För in resultatet i tabellen vid det uppmätta avståndet.
Till de upmätta avstånden måste adderas avståndet
mellan källa och detektor när källan är inskjuten så
långt som möjligt. Detta avstånd är för både
GammaData's och för Risø's alfakälla 1,1 cm.
Om man vill mäta om ett avstånd, kan man nollställa spektrumet
med kommandot NOL. Det behövs också om man vill mäta
några punkter till med mindre intervall vid räckviddens slut. Med kommandot GRA kan grafen skrivas ut.
| Läge (cm) | Avstånd (cm) | Centroid (kanal) |
|---|---|---|
Rita ett diagram över centroiden som funktion av avståndet, till exempel med programmet Graphical Analysis. Rita en graf som ansluter snyggt till mätpunkterna och extrapolera den till y-axeln. Denna skärning med axeln motsvarar alfa-partikelns initiella energi. Med litteraturvärdet för den vanligaste alfa-energi från Am-241 kan man nu även skriva energiskala längs y-axeln. Vi förutsätter att "kanal 0" motsvarar "energi 0". (I Risø's alfakälla har det radioaktiva materialet en beläggning som bromsar alfa-partiklarna redan i källan.)
Beräkna genom att extrapolera grafen i ditt diagram till x-axeln hur lång räckvidden är i luft för dessa alfapartiklar. Jamför dina resultat med literaturvärden, t ex i Physics Handbook, F-8.6.
Riktningskoefficienten för (tangenten till) kurvan ger energiförlusten per längdenhet i luft. Energiförlusten per längdenhet (-dE/dx) brukar på svenska kallas bromsförmåga. Genom att beräkna bromsförmågan vid olika avstånd från källan, dvs riktningskoefficienten till grafen i diagrammet, kan man konstruera den sk Braggkurvan, vilken är en graf som visar bromsförmågan som funktion av den sträcka som partikeln gått i mediet.
Rita ett diagram över bromsförmågan som funktion av avståndet.
Som du ser varierar bromsförmågan med sträckan som α-partikeln färdats. Ju lägre rörelseenergi hos alfapartikeln, desto större bromsförmåga. Bromsförmågan är som störst i slutet av partikelbanan. Ökningen av bromsförmågan i partikelbanans slut syns i diagrammet som en topp, "Braggtoppen". Innebörden av Braggtoppen är att mot slutet av partikelbanan avges mycket energi per längdenhet. Detta utnyttjas inom strålterapin för att skada en tumör maximalt men samtidigt skona omgivande vävnad.
Som källa använder vi cesium-137 med en aktivitet på 370 kBq = 10 μCi. Beta-sönderfall ger ett exciterat tillstånd av Ba-137 som ger gammastrålning med en energi på 661,7 keV. Detektorn är ett Geiger-Müller-rör. Röret är fyllt med gas, och de allra flesta gamma-fotonerna går rakt igenom. Men några av fotonerna joniserar en gasmolekyl. Elektronen acceleraras då av det höga elektriska fältet nära elektroden mitt i GM-röret, och slår då ut elektroner ur andra molekyler. Förstärkningen ger en lavin av typ 1010 elektroner, som är en elektroniskt detekterbar laddningspuls. Pulsens höjd har inget samband med gamma-fotonens energi.
Ställ γ-källan och GM-röret in på samma höjd. Det går lättast om de står nära varandra. Flytta nu ryttarna isär så att man kan hänga blyplattor på källans hållare.
Mät detektorns räknehastighet (t ex antalet pulser i en minut) som funktion av antalet blyplattor mellan källa och detektor. Mät blyplattornas tjocklek. Kolla även hur mycket strålning absorberas när du håller din hand eller ditt finger emellan (det räcker med att mäta i 10 sekunder). Bestäm även backgrundstrålningen: ta bort strålningskällan och låt räknaren gå en längre tid (minst 5 minuter). Glöm inte mäta tiden.
Rita mätvärden i en graf, till exempel med programmet Graphical Analysis. Subtrahera bakgrundsintensiteten. Bestäm halveringstjockleken och absorptionskoeffiecienten. Enklast går det genom att anpassa en exponentiell funktion till mätpunkterna med ett dataprogram. Men man kan också rita mätvärdenas logaritm som funktion av antalet plattor, och bestämma lutningen av en regressionslinje. Bestäm halveringstjockleken ur koefficienterna.
Jämför med literaturvärden, t ex från Physics Handbook F-8.5.