För att dispergera solljusets olika färger i olika vinklar kan man använda ett prisma eller ett dispersionsgitter. Prismer är inte praktiska för röntgenstrålning, eftersom alla material har en brytningsindex n≈1 i röntgenområdet. Ristade gitter är praktiska endast för de mjukaste röntgenvågländerna. För hårdare rötngenstrålning kan man använda kristallgitter, där avståndet mellan atomerna är jämförbar med röntgenstrålningens våglängd.
För att monokromatisera ultraviolet eller mjukröntgenstrålning kan man diffraktion från använda ristade gitter i reflektion. (Det finns inga transparanta material i det här området, så et är svårt att göra transmissionsgitter.) Eftersom vågländen är kortare än vad man kan rista mekaniskt eller fotokemiskt, måste man använda glänsande infallsvinklar. Ett annat skäl är att reflektiviteten i det här våglängdsområdet är nästan noll vid vinkelrätt infall.
Metoden lämpar sig för högupplöst spektroskopi, se till exempel denna beskrivning av en röntgenspektrometer. Metoden är inte praktiskt för våglängder kortare än en nanometer (energier högre än 1000 eV).
Max von Laue upptäckte år 1912 att kristaller kan ge upphov till diffraktion av röntgenstrålning. Ett år senare insåg Bragg att man kunde tolka diffraktionsmönstret som reflektion av kristallplan. Han härledde
där d är avståndet mellan atomplan, θ är den glänsande infallsvinkeln, λ är röntgenvåglängden och n=1,2,3,... är diffraktionsordningen.

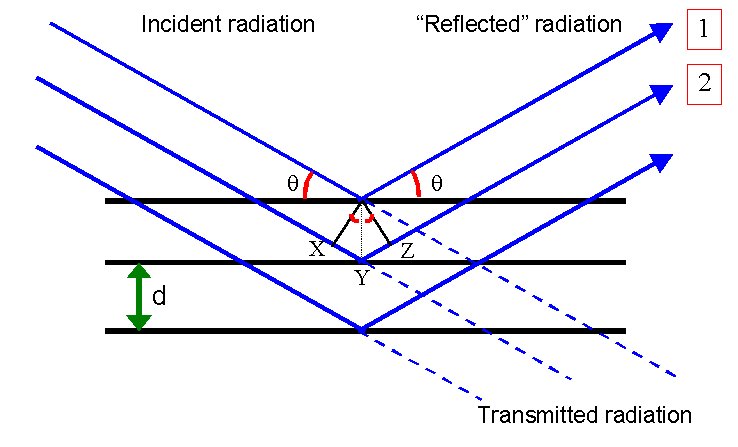
Det är bara när Braggvillkoret är uppfyllt, att de reflekterade strålarna interfererar konstruktivt, eftersom vägskillnaden XYZ (se figur) är lika med ett helt antal våglängder. Då är reflektionerna från alla tusentals plan i fas med varandra, och ger en stark reflektion.
Om man varierar infallsvinkeln θ, kan man mäta den Bragg-reflekterade strålens intensitet som funktion av θ. När källan är stationnär, rotarerar man kristallen och detektorn kopplade i &theta-2&theta-mod. Om man vet planavståndet d, får man då ett spektrum - en kurva av röntgenkällans intensitet som funktion av våglängd.
Man kan också använda Braggs lag för att bestämma kristallstrukturen. Om man vet röntgenvåglängden (till exempel källans Kα våglängd), kan man bestämma planavståndet d ur en vinkelscan.