
Laborationen studerar absorption av alfa-strålning i luft. Alfa-strålning består av partiklar, heliumkärnor, med hög kinetisk energi. De kommer från tunga positiva atomkärnor, där deras potentiella Coulomb-energi är hög (typiskt värde 5 MeV). När dessa partiklar färdas genom luft, förlårar de energi genom att jonisera luftmolekyler. De bromsas upp på ungefär samma sätt som en bil som stannar. Alfa-partiklar beter sig alltså annorlunda än gammastrålning som är elektromagnetisk strålning med extremt hög frekvens. Den kan också beskrivas som fotoner. Absorption av fotoner är en slumpprocess. Intensiteten avtar exponentiellt I = Ioe-μx, där μ=ln 2/τ½ är den lineara absorptionskoefficienten ( Lamberts lag, samma formel som för synligt ljus och annan elektromagnetisk strålning).

Mätinstrumentet är en alfa- och betadetektor av Gammadata (den röda lådan på bilden). Alfa-källan sitter på en lång metallstav och består av americium-241, samma grundämne som i brandvarnare. Isotopens halveringstid är 432 år och alfa-energin är 5,5 MeV. Detektorn är en ytbarriärdetektor. För varje alfapartikel ger den en puls vars höjd är proportionell mot alfapartikelns kinetiska energi. Signalen digitaliseras med datorns ljudingång och analyseras av programmet PRA av Marek Dolleiser. Den röda lådans β-utgång är modifierad för att matcha ludingångens maxfrekvens. På datorn kan man då se en graf av alfa-partiklarnas energifördelning. Om man ökar avståndet mellan det radioaktiva preparatet och detektorn, blir energiförlusten i luften större. Den energi som detekteras blir alltså lägre. |
Enligt Born-Bethe-formeln minskar energin per längdenhet invers proportionellt mot partikelns energi. Partiklarnas energiförluster är alltså störst mot slutet av deras räckvidd, när den kinetiska energin är liten. Denna topp i grafen av energieförlust mot avstånd kallas Bragg peak.
Om energiminskningen skulle följa Born-Bethe exakt, kan man härleda att energin borde bero på avstånd som E = E0 √ L - x över räckvidden L (se en .pdf-fil). Men det stämmer inte helt bra med experiment. År 1910 använde Geiger den empiriska formeln E = E0 (L-x)2/3, alltså en exponent 0,667 istället för 0,5.
Den radioaktiva källan som undersöks är 241Am med en aktivitet på 10 kBq.
Starta programmet PRA på datorn. Egentligen är det programvara för Windows, men vi kör det på Macintosh under Crossover. Starta programmet genom att klicka på PRA-ikonen i mappen PhysicsLab. Det ska komma upp ett fönster med en liten meny. Välj under View att också visa Pulse Height Histogram och Audio Input. För att se audiosignalen måste man start datainsamlingen under tab Action. Man ser då att stereo-signalen i audio-fönstret (röd för vänster, grön för höger) ändrar sig.
Placera alfakällan i den röda detektionslådan och skjut den inåt. I audio-fönstret ska man då se negativa pulser. Om signalen är för liten, behöver man kanske vrida upp ljudet under systeminställningarna i OS X. Ställ brytaren i läge "β". Det första som man måste göra är att programmet måste lära sig formen på pulserna. Under Settings klicka på Data Acquisition and Analysis och skriv ett negativt värde för Height threshold för vänsterkanalen under Pulse recognition. After Apply ser man då en gul linje. Tröskelvärdet är inte kritiskt, ska bara ligga under toppvärdet av pulserna som man vill detektera. Kryssa också för Use shape tolerance method.
Det kan vara för många pulser när provet är närmast, så att pulser börjar ibland överlappa varandra. Därför kan dat vara bra att dra staven någon centimeter utåt. Klicka sedan under Action-menyn på Start pulse shape acquisition. I histogrammet på datorskärmen ska det nu växa upp en topp någonstans på histogrammets högre halva. Om det är tillräckligt många counts (efter några sekunder), kan du stoppa insamlingen genom att klicka Stop Acquisition. Det kommer upp en Edit pulse shape dialog - godkänn.
Nu kan man mäta pulshöjdsdiagram under Action-meny eller genom att pressa tangenten "A". Man kan också lyssna på pulshöjderna, igen via Action-meny eller genom att pressa mellanslagstangenten. Flytta staven fram och tillbaka, se och lyssna på vad som händer. Minska tröskelvärdet så mycket som det går utan att det blir för mycket brus.
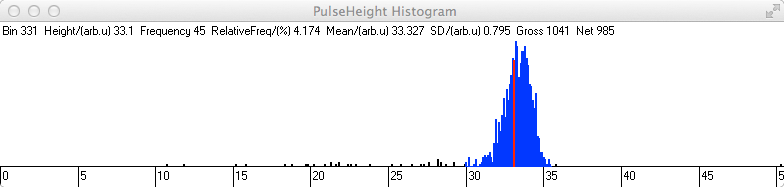
Gör nu för ett antal avstånd följande och mät läget med skjutmått. Starta data-insamling, definiera en ROI (region of interest) i histogrammet genom att kontroll-klicka och dra från vänster till högersida av toppen i histogrammet - den får då en färg. Positionera sedan kursor någonstans inom ROI. Kanalen blir röd och programmet räknar ut centroiden av ROI (se skärmbild ovan). För in resultatet i tabellen vid det uppmätta avståndet. Till de upmätta avstånden måste adderas avståndet mellan källa och detektor när källan är inskjuten så långt som möjligt. Detta avstånd är 1,1 cm.
| Läge (cm) | Avstånd (cm) | Centroid (kanal) |
|---|---|---|
Rita ett diagram över centroiden som funktion av avståndet, till exempel med programmet Logger Pro. Använd skalning från noll för axlarna. Anpassa Geigers empiriska funktion till mätpunkterna. Kurvans skärning med y-axeln motsvarar alfa-partikelns initiella energi. Med litteraturvärdet för den vanligaste alfa-energi från Am-241 kan man nu räkna om kanalnummer till en energiskala. Vi förutsätter att "kanal 0" motsvarar "energi 0". (Och vi försummar att alfakällan har en beläggning som bromsar alfa-partiklarna redan i preparatet.) Gör nu ett nytt diagram med energi i MeV som funktion av avstånd.
Extrapolering till x-axeln ger räckvidden i luft för dessa alfapartiklar. Jamför dina resultat för ett antal energier med literaturvärden, t ex i Physics Handbook, F-8.6.
Riktningskoefficienten för (tangenten till) kurvan ger energiförlusten per längdenhet i luft. Energiförlusten per längdenhet (-dE/dx) brukar på svenska kallas bromsförmåga. Beräkna Braggkurvan, vilken är en graf som visar bromsförmågan som funktion av den sträcka som partikeln gått i mediet. Rita diagrammet.
Som du ser varierar bromsförmågan med sträckan som α-partikeln färdats. Ju lägre rörelseenergi hos alfapartikeln, desto större bromsförmåga. Bromsförmågan är som störst i slutet av partikelbanan. Ökningen av bromsförmågan i partikelbanans slut syns i diagrammet som en topp, "Braggtoppen". Innebörden av Braggtoppen är att mot slutet av partikelbanan avges mycket energi per längdenhet. Detta utnyttjas inom strålterapin för att skada en tumör maximalt men samtidigt skona omgivande vävnad.